Small Angle Approximation in MPC Kinematic Model

Hi friends! I kind of have a lot going on right now between Term 3, job hunt stuff (I’m already in talks with a few companies - squee!), being sick, and getting ready to have a couple of teeth pulled (yuck!), so I’m totally copping out on this week’s blog post and more or less pasting an e-mail conversation I had yesterday with my new friend Shubham. It’s good stuff, though! Fair warning: if you e-mail me I reserve the right to make a blog post out of our conversation and take whatever liberties necessary to cast myself in the best light possible - ha!

Shubham:

Hi Jeremy,
How are you doing? I am Shubham and I was looking at your MPC code that you did for Udacity self driving car Nanodegree. You have given a very nice explanation of the system kinematics and the constraints.

In the explaination on github, I think there is some correction in the update of orientation of bicycle model. I think it should be:

I think you are missing the tan(delta) in your explanation and your code. I might be wrong but please can you check it and provide me with explanation regarding that? I am very much interested in MPC.
Looking forward to your reply.

Me:

Thanks for pointing that out Shubham. I kind of took Udacity at their word (although I admit I should have been skeptical that the yaw rate could be so simply derived from the steering angle). They did present more complex dynamic motion models in the lessons (without going into detail), but said they might be less tractable than the simplified kinematic models we were given. Looking at this paper, on page 27 (13 of the pdf) the yaw rate equation includes a few extra terms that Udacity threw out (I believe they already assume the slip angle and rear steering angle are zero) but it does include the tangent you’re talking about.

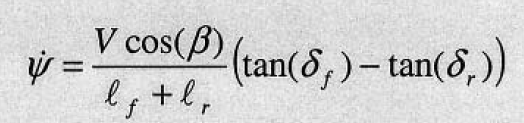
As far as removing the tangent… maybe they are using the small angle approximation (i.e. tan(x) = x). I presume they were just trying to simplify it as much as possible, since we’re only applying it in a simulator.
I’d love to hear your thoughts, though.

Shubham:

Hi Jeremy,
I think the small angle approximation will only work if your steering angle is very less in case of straight line trajectories and very smooth curvatures(very high high radius). Even I thought about small angle approximation but I think it is a very loose assumption considering the simulator has some really strong turns. Also for a car approximating as bicycle model, at low speeds (normal speeds) the rear wheel does not have much angle of its own so I think that is a good assumption. I have not taken the Udacity course but have they assumed the same model (without the tangent) in the lectures?
Thanks and Regards,
Shubham

Me:

Well, since the simulator (or perhaps it’s just our constraints) limits the steering angle to (-25,25) degrees, I think the small angle approximation should suffice (see the image below). Here’s the code that sets that constraint:

// The upper and lower limits of delta are set to -25 and 25
// degrees (values in radians).
// NOTE: Feel free to change this to something else.
for (int i = delta_start; i < a_start; i++) {
   vars_lowerbound[i] = -0.436332;
   vars_upperbound[i] = 0.436332; 
}

I imagine they wanted to relieve the optimizer as much as possible.
The model equations I used in my blog (the ones that you attached in your original e-mail) were taken directly from the Udacity lectures. They never included the tangent in the yaw rate… probably just to keep things simple for us, but I might ask about it in the forum. Where did you find your model equations (that include tangent)?

Shubham:

Hi Jeremy,
Yes I think if the limits are -25 to +25 then it would not make any difference. I got the model with the tangent from MPC lab at UC Berkeley.

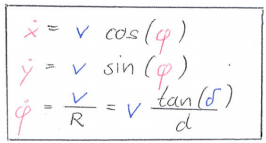
This is a kinematic model and is good for simulation purposes.
Hope it helps.

Me:

Thanks Shubham. I see that those notes mention parking (I assume for some kind of parking assist), and in that case I bet you would see steering angles well above 25 degrees. Interesting! Thanks for sharing.

I did post this conversation in the Nanodegree forum, by the way. The consensus thus far is that, yes, we are seeing the result of a small angle approximation. Another forum member linked to yet another academic paper that suggests a more robust model will indeed include the tangent of the steering angle in determining the yaw rate. Thanks to Shubham for the insightful exchange (and an excuse to put some always-impressive Greek letters on my blog)!